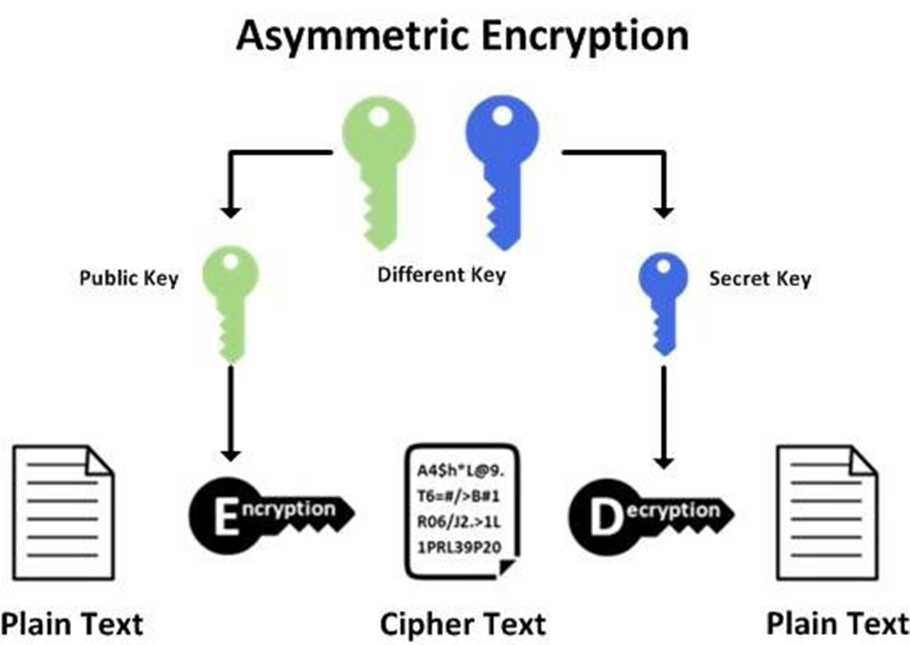
RSA (Rivest–Shamir–Adleman) is one of the first public-key cryptosystems and is widely used for secure data transmission. It’s also used in TLS handshake. The foundation of RSA lies in asymmetric encryption, where a key pair is involved. Specifically, data encrypted with a private key can be decrypted using the corresponding public key, and vice versa.
Euler Phi
Before deep dive to the RSA, we need some math to understand the key generation process.
What is co-prime number
The co-prime numbers are the pair of numbers that only have 1 common factor is 1. For example, 7 and 2 are co-prime numbers.
Euler Phi
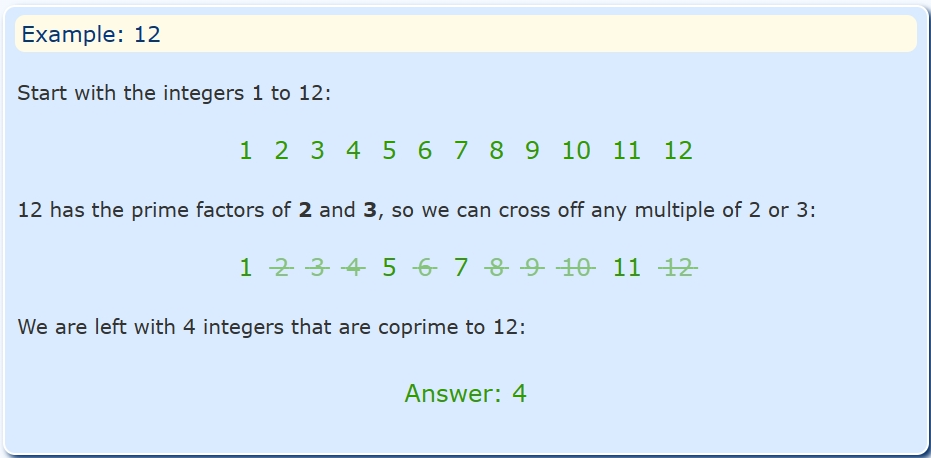
Picture 1. Euler Phi example
If you want get more detail about the Euler Phi please refer to this link: Euler’s Totient Function (mathsisfun.com)
Key Generation
Following the steps below to generate the keys:
- Select 2 prime numbers p, q. Calculate N = p*q.
- Euler Phi calculation Φ(N) = (P-1)(Q-1).
- Select e: 1< e < Φ(N), co-prime with N, Φ(N).
- Select d: d*e (mod Φ(N)) = 1.
- Finally, we get the publish key (e, N) and private key (d, N).
For example:
- Select 2 prime numbers: p = 2, q = 7.
- Euler Phi calculation Φ(14) = (2-1)(7-1) = 6.
- Select e: 1< e < Φ(14), co-prime with 14, Φ(14) -> e = 5.
- Select d: d*e (mod Φ(N)) = 1 <=> 5*d (mod 6) = 1 -> d = 11.
- Publish key is (5, 14), private key is (11, 14).
Encryption/Decryption
Encryption with private is (d, N).
Decryption with publish key is (e, N).
Example
Sender side: original text: B – 2, private key (11, 14)
Receiver side: publish key is (5, 14)
In the real world, the private key and the public key are large numbers (e.g. 2048 bits long) for more security. In this topic, I just used small numbers to see how the RSA works. Thanks for reading!
