In the preceding sections, we explored the concept and properties of Elliptic Curve Finite Fields. In this topic, we dive into an application of the Elliptic-Curve Diffie–Hellman (ECDHE) which is the TLS handshake mechanism.
Generalized Discrete Logarithm Problem (GDLP)
For example, we have 2 colors red and yellow then mix them. We easily get the orange color. But reverting orange color to red and yellow is difficult. That is the idea of GDLP.
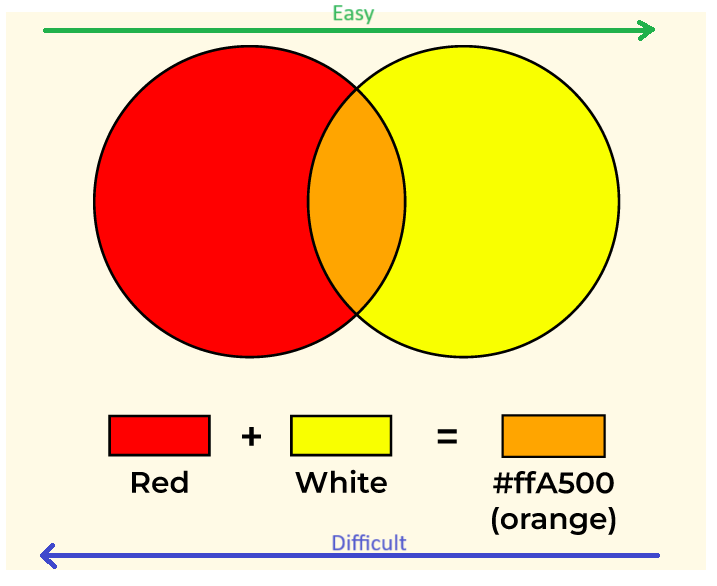
Picture 1: color example
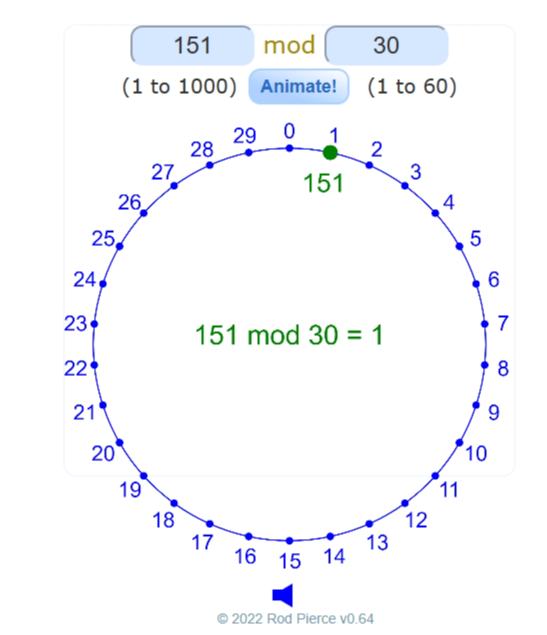
Picture 2: Cyclic group
When both x and p are very large, it is easy to determine b when we know the value of x. However, the reverse finding x when we know b is very hard.
The Generalized Discrete Logarithm Problem in the Elliptic Curves Finite Field is similar.
Finding R is easy when know x. However, it’s hard to find x if know R.
Elliptic-Curve Diffie–Hellman (ECDHE)
We have 4 steps to exchange the key using ECDHE.
- Choose the elliptic curve finite field and the generator G is a point belonging to the curve.
- Select the private key a and b.
- Calculate and share the secret path – Alice’s side: Ka = a*G, Bob’s side: Kb = b*G
- Session key calculation Kc = Ka*b = Kb*a = a*b*Kc

Picture 3: Key exchange using ECDHE
After thoroughly discussing ECDHE, I think we’ve covered all the essential points. If you have any further questions or corrections, feel free to ask me in the comments.
Thanks for reading!
