[SSL/TLS] Part 2 – Diffie-Hellman

Have you ever wondered how two parties can securely communicate online without revealing their secrets to anyone else? How can they agree on a common key to encrypt and decrypt their messages, without sending the key over the network? This is where the Diffie-Hellman key exchange comes in handy.

The key exchange algorithm used in Part 1 is Diffie-Hellman.

How does it work?

Alice and Bob

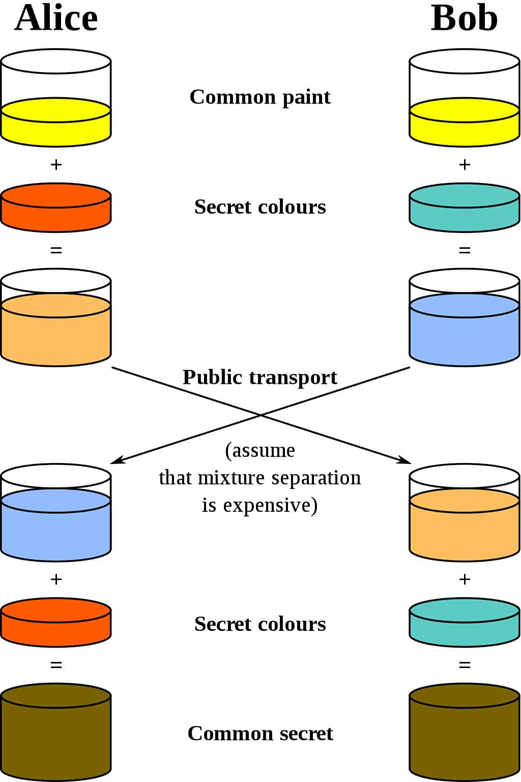
Picture 1. Alice and Bob example

Let’s take a common example on the internet Alice and Bob. Alice has a secret red color and Bob has a secret green color. Next, they combine their color with a common color (yellow) and then send the results to each other. Finally, they combine the received color with their secret color to get the common secret color. That is the way the Diffie-Hellman works.

The common secret color is also called the symmetric key. That means the message sent from Alice to Bob is encrypted and decrypted by only one key.

Key exchanging in mathematics

1. Choose the modulus (p) and base (g).
2. Select the secret numbers a and b
3. Pubic transport, Mixing color: g^a mod p and g^b mod p.
4. Common secret calculation (the symmetric key).

Example:

1. Choose the modulus (p) and base (g).
   (p) is 17, while the base (g) is 4.
2. Select the secret numbers a and b
   Alice: a = 3
   Bob: b = 6
3. Pubic transport, Mixing color:
   A = g^amod p = 4³ mod 17 = 13
   B = g^bmod p = 4⁶ mod 17 = 16
   Alice and Bob send A and B to each other.
4. Common secret calculation (the symmetric key).
   Alice: s = B^a mod p = 16³ mod 17 = 16
   Bob: s = A^b mod p = 13⁶mod 17 = 16
   So the Common secret (session key) is 16.

Thanks for reading!