Digital Signature Algorithm

What is a digital signature?

In the physical world, document verification is done through signatures. For example, if you send me a document with your signature, I trust its authenticity because of that signature. Similarly, on the internet, document verification is achieved using digital signatures.

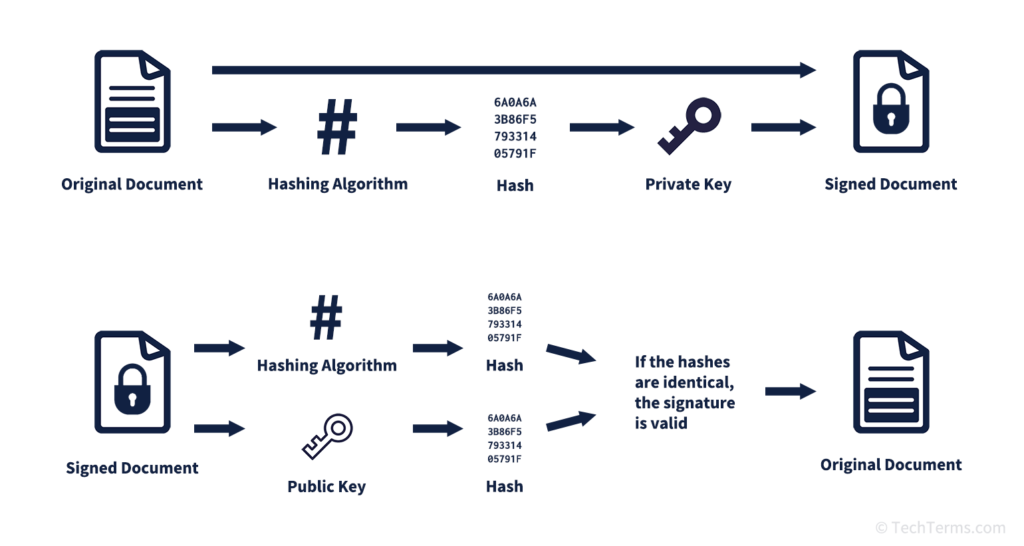
Picture 1. DSA block diagram

Sender

From the original document, the Sender uses a hash function to generate the hash value H(m). After that, the Sender then signs H(m) to create a signature S. Next, the Sender encrypts both original document and the signature S with his private key (this private key that used in TLS handshake for example) before sending them to the Receiver.

Receiver

After receiving the encrypted message, the Receiver decrypts it to retrieve the signature S and the original document. Subsequently, the Receiver performs the verification base on the signature S original document if the result is true, then the original document is valid.

Little bit about hash

Hashing is a process that converts the variable-size input to a fixed-size output. To play around with hashing please refer to this link.

This is complicated part so I don’t go more detail in this topic. If you are curious about how does the hashing function work please deep dive to these links MD5, SHA.

DSA Operations

DSA operation involves 4 steps

1. Key generation
   • Parameter generation
     • choose hash function (SHA-1, SHA-2) with output length |𝐻| bits.
     • Choose a key length L. The original DSS constrained L to be a multiple of 64 between 512 and 1024 inclusive. . NIST 800-57 recommends L=2048.
     • Choose the modulus length N such that N<L and N≤|𝐻|. FIPS 186-4 specifies the values (L, N): (1024, 160), (2048, 224), (2048, 256), or (3072, 256).
     • Generate a random prime number q from N-bits.
     • Choose an L-bit prime p such that p-1 is a multiple of q.
     • Choose an integer h randomly from {2…p−2}.
     • Compute g = h^(p-1)/q. In the rare case that g=1 try again with a different h. Commonly h=2 is used.
     • The algorithm parameters are (p, q, g).
   • Per-user keys
     • Given a set of parameters, the second phase computes the key pair for a single user.
     • Private key is an integer x randomly from {1…q−1}.
     • Public key y = g^x mod p.
2. Key distribution
   Sender send private key to receiver.
3. Signing process with message m
   • choose k randomly from {1…q−1}.
   • Compute r = (g^k mod p) mod q.
   • Compute s = (k^-1 (H(m) + xr)) mod q.
   • In the case r = 0 or s = 0, start again with a different k.
     The signature is (r, s).
4. Signature Verification
   • Verify that 0 < r < q and 0 < s < q
   • Compute ω = s^-1 mod q
     From s = (k^-1 (H(m) + xr)) mod q.
     We have k = H(m)s^-1 + xrs^-1 = H(m)ω + xrω (mod q)
   • Compute µ1 = H(m)ω mod q
   • Compute µ2 = r. ω mod q
   • Compute g^k = g^H(m)ωg^xrω= g^H(m)ωy^rω= g^µ1y^µ2 (mod p)
     Call v = g^µ1y^µ2 mod q is the signature computed by receiver.
   • We have r = (g^k mod p) mod q = (g^µ1y^µ2 mod p) mod q = v
     Now we have r=v so the signature is valid.

Enough complicated math, so we end the topic here. Thanks for reading!